算法是計算的命脈。它們是電腦解決問題、分析資料和做出決策所遵循的逐步指令。就像食譜一樣，它們將複雜的任務分解為易於管理的程式。理解這些基本演算法是掌握電腦科學和程式設計的基石。

什麼是演算法

1. 搜尋演算法：

什麼是搜尋？

搜尋是在資料集合中定位特定元素或專案的基本過程。此資料集合可以採用各種形式，例如陣列、列表、樹或其他結構化表示。搜尋的主要目標是確定資料中是否存在所需元素，如果存在，則辨識其精確位置或檢索它。它在各種計算任務和現實應用中發揮重要作用，包括資訊檢索、資料分析、決策過程等。

介紹搜尋演算法

所有搜尋演算法都使用搜尋關鍵字來繼續執行該過程。搜尋演算法預計會返回成功或失敗狀態，通常以布林 true/false 表示。可以使用不同的搜尋演算法，其效能和效率取決於資料及其使用方式。

線性搜尋演算法被認為是所有搜尋演算法中最基本的。最好的也許是二分搜尋。還有其他搜尋演算法，例如深度優先搜尋演算法、廣度優先演算法等。搜尋演算法中使用的符號是 O(n)，其中 n 是完成的比較次數。它給出了演算法在給定條件下所需執行時間的漸近上限的概念。

搜尋演算法中的搜尋案例可以分為最佳情況、平均情況和最壞情況。在某些演算法中，所有三種情況可能漸近相同，而在其他一些演算法中可能存在很大差異。搜尋演算法的平均行為有助於確定演算法的有用性。

摘要： 搜尋演算法是用於在資料集合中定位特定資料的逐步過程。它被認為是計算中的基本過程。在電腦科學中，搜尋資料時，快速應用程式和較慢應用程式之間的差異通常在於使用正確的搜尋演算法。

術語：

• 目標元素：這就是你要尋找的寶藏！這是您想要在集合中尋找的特定資料。想像搜尋電話簿 - 目標元素是特定人的電話號碼。

• 搜尋空間：將其視為可能隱藏針的大海撈針。它代表您正在搜尋的整個資料集合。這可以是數字陣列、名稱列表或更複雜的資料結構。

• 複雜度：這是指搜尋演算法所需的工作量。這就像衡量圖書館員需要做多少工作才能找到你的書。複雜性通常以時間（找到目標需要多長時間）和空間（演算法需要多少額外記憶體）來衡量。

• 確定性與非確定性：搜尋演算法可以像遵循食譜（確定性）或進行有根據的猜測（非確定性）。確定性演算法始終遵循相同的清晰步驟，例如二分搜尋，它將搜尋空間一分為二。非確定性演算法（例如線性搜尋）可能需要在最壞的情況下檢查整個集合。

實際應用

• 資訊檢索：想像在網路上搜尋特定的食譜。像Google這樣的搜尋引擎利用複雜的搜尋演算法來篩選大量資料集，為網站和內容建立索引。當您輸入查詢時，這些演算法會辨識與您的搜尋字詞最相關的網頁，並在幾分之一秒內提供您要尋找的資訊。

• 資料庫系統：資料庫儲存大量訊息，從客戶記錄到金融交易。搜尋演算法是高效資料檢索的支柱。當您在資料庫管理系統中提交查詢時，搜尋演算法會快速找到符合您條件的特定記錄，從而節省您的時間和精力。

• 電子商務：線上購物因高效搜尋而蓬勃發展。電子商務平台使用搜尋演算法來幫助您找到完美的產品。它們允許您根據價格、品牌或顏色等各種標準進行過濾和搜尋。在幕後，搜尋演算法為這些過濾器提供支持，精確定位滿足您偏好的產品，使您的購物體驗順暢高效。

• 網路：網路是一個由互連設備組成的複雜網路。搜尋演算法在有效路由資料包方面發揮著至關重要的作用。它們可協助確定訊息在網路上傳輸的最佳路徑，確保您的視訊通話或線上遊戲順利運作。

• 人工智慧（AI）：人工智慧正在為許多領域帶來革命性的變化。搜尋演算法是人工智慧應用的基本工具。它們使人工智慧系統能夠解決問題、做出決策，甚至玩國際象棋等遊戲。透過有效地搜尋大量資料並辨識模式，搜尋演算法有助於人工智慧背後的智慧。

• 模式辨識：模式辨識允許電腦辨識和理解資料中的模式，例如圖像、語音或手寫。搜尋演算法對於模式辨識很有幫助。它們可協助電腦將新資料與現有模式進行匹配，從而實現照片中的臉部辨識或虛擬助理的語音辨識等應用。

演算法類型：

1. Linear Search ：

想像一下，在一個雜亂無章的書架中尋找一本特定的書。線性搜尋模仿了這種方法。這是一種簡單的方法，可以逐項檢查集合中的每個專案，直到找到目標元素（您想要的書）。

它的工作原理如下：

1. 搜尋從集合中的第一項開始。

2. 此演算法將目標元素與目前專案進行比較。

* If they match, the search is successful, and the algorithm returns the location (index) of the target element.

* If they don't match, the algorithm moves on to the next item in the collection.

3. 這種比較和移動的過程將持續下去，直到找到目標元素或耗盡整個集合。

例子：

讓我們在未排序清單中搜尋值「25」：[10, 4, 12, 25, 18, 7]。

• 搜尋從第一個元素 (10) 開始。由於 10 不是 25，我們繼續。

• 我們將目標 (25) 與下一個元素 (4) 進行比較。沒有匹配項，所以我們繼續。

• 重複此過程，直到到達索引 3 處的元素「25」。

優勢：

• 易於理解和實施，使其成為初學者的好選擇。

• 適用於未排序的資料，在各種情況下提供靈活性。

弱點：

• 對於大型資料集來說速度很慢。隨著集合大小的增加，搜尋時間也會成比例增加，導致海量資料集效率低。

怎麼運作的 ：

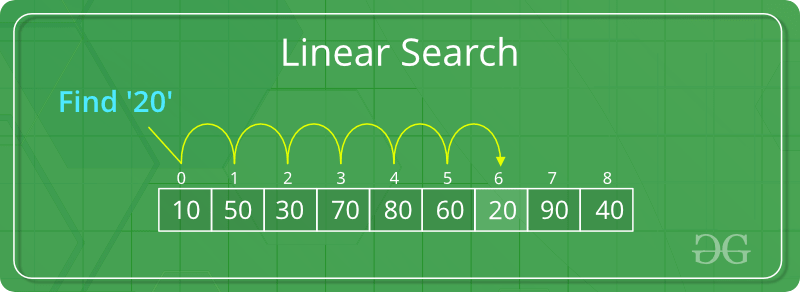
2. Binary Search ：

二分搜尋在排序資料上蓬勃發展。想像一下在一本精心組織的字典中搜尋特定單字。在這種情況下，二分搜尋比線性搜尋快得多。它透過重複地將已排序的集合分成兩半來進行操作。策略如下：

1. 此演算法首先將目標元素與集合的中間元素進行比較。

2. 如果目標元素等於中間元素，則搜尋成功，演算法會傳回中間元素的索引。

3. 如果目標元素小於中間元素，則在剩餘集合的左半部（不包括中間元素）繼續搜尋。

4. 如果目標元素大於中間元素，則在剩餘集合的右半部繼續搜尋。

5. 在集合的縮小範圍的一半上重複步驟 1-4，直到找到目標元素或搜尋空間減少到單一元素（與目標不符）。

例子：

讓我們在排序清單中搜尋值「18」：[4, 7, 10, 12, 18, 25]。

• 中間的元素是 12。

• 現在，右半部的中間元素是18。目標元素位於索引 4 處。

優勢：

• 對於大型排序資料集，比線性搜尋快得多。透過在每次比較時消除一半的剩餘元素，二分搜尋可以快速縮小搜尋空間。

弱點：

• 要求預先對資料進行排序，如果資料尚未組織，則加入額外的步驟。

• 不適合未排序的資料。二分搜尋策略依賴資料的排序性質，以在每次迭代期間有效地消除一半的可能性。

怎麼運作的 ：

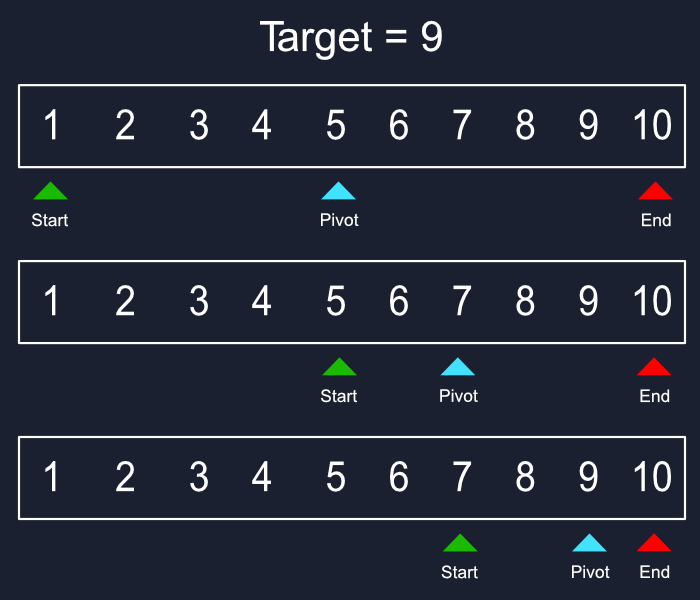
2. 排序演算法：

什麼是排序？

排序是指根據元素上的比較運算子對給定陣列或元素列表進行重新排列。比較運算子用於決定對應資料結構中元素的新順序。排序意味著將所有元素按升序或降序重新排序。

介紹

在計算機科學中，排序演算法是將列表中的元素依序排列的演算法。最常用的順序是數字順序和字典順序，以及升序或降序。高效排序對於優化需要輸入資料位於排序清單中的其他演算法（例如搜尋和合併演算法）的效率非常重要。排序對於規範化資料和產生人類可讀的輸出通常也很有用。

形式上，任何排序演算法的輸出必須滿足兩個條件：

輸出是單調順序的（根據所需的順序，每個元素不小於/大於前一個元素）。

1. 輸出是輸入的排列（重新排序，但保留所有原始元素）。

2. 為了獲得最佳效率，輸入資料應儲存在允許隨機存取的資料結構中，而不是僅允許順序存取的資料結構中。

摘要：排序演算法是一組指令，它將陣列或列表作為輸入並將專案排列成特定的順序。排序最常見的是數字或字母（或字典）順序，並且可以按升序（AZ，0-9）或降序（ZA，9-0）。

術語：

• 就地分類：想像一下重新整理抽屜裡的衣服而不把所有東西都拿出來。就地排序的工作原理類似。這些演算法透過修改現有清單本身內元素的順序來對資料進行排序，從而需要最少的額外空間。例如選擇排序、冒泡排序和插入排序。

• 內部排序：這是指完全在電腦主記憶體 (RAM) 內執行的排序演算法。整個資料集可以一次載入到記憶體中，使其適合中小型資料集。堆排序、冒泡排序和合併排序等內部排序演算法通常用於記憶體資料操作。

• 外部排序：當處理超出主存容量的海量資料集時，外部排序就發揮作用。這些演算法將大型資料集分解為較小的區塊，在磁碟（輔助儲存）上對它們進行排序，然後按特定順序將排序後的區塊合併在一起。合併排序是外部排序演算法的一個流行範例。

• 穩定排序：想像一下按標題對書籍清單進行排序，但您也希望保留具有相同標題的書籍最初列出的順序。穩定的排序演算法在排序過程中保持具有相等鍵（值）的元素的相對順序。歸併排序和插入排序是穩定排序演算法的範例。

• 不穩定排序：並非所有排序演算法都優先考慮順序保留。不穩定的排序演算法僅專注於實現所需的排序順序（例如，升序或降序），並且可能會打亂具有相同鍵的元素的相對位置。快速排序和堆排序是不穩定排序演算法的例子。

排序演算法的特徵：

• 時間複雜度：這是指排序演算法完成其工作所需的時間（以步驟或比較而言）。我們通常在三種情況下分析時間複雜度：

* **Worst-case:** This represents the maximum amount of time the algorithm could take for a particular data size, considering the worst possible input scenario.

* **Average-case:** This reflects the average time the algorithm takes across various random inputs of the same size.

* **Best-case:** This represents the minimum amount of time the algorithm could take for a specific data size, considering the most favorable input scenario (e.g., data already partially sorted).

• 空間複雜度：這是指排序演算法在原始資料所佔用的空間之外執行其操作所需的額外記憶體量。就地排序演算法透過在現有記憶體分配中操作資料來使用最少的額外空間，而某些演算法在排序過程中可能需要額外的臨時儲存。

• 穩定性：此屬性決定排序演算法是否保留排序輸出中具有相等值的元素的原始順序。穩定的排序演算法維護這些元素的相對位置，這在特定應用中可能很重要。例如，如果您按姓名對客戶記錄清單進行排序，並且兩個客戶具有相同的姓名，您可能需要穩定的排序來維護它們最初列出的順序（例如，按帳戶建立日期）。

• 就地排序：如前所述，就地排序演算法非常節省內存，因為它們透過修改原始列表本身來對資料進行排序，從而需要最少的額外空間。當處理大型資料集或記憶體有限時，這可能是有利的。

• 適應性：一些排序演算法可以適應它們正在排序的資料的特徵。自適應排序演算法可以利用資料中預先存在的順序來提高其效能。例如，如果資料已經部分排序，自適應演算法可能會調整其方法以利用該部分順序並實現更快的排序。

排序演算法的應用：

• 搜尋演算法：想像在電話簿中搜尋特定聯絡人。排序演算法是二分搜尋等高效搜尋演算法的無聲夥伴。透過確保電話簿條目按字母順序組織（排序），二分搜尋可以比透過未排序清單的線性搜尋更快找到您的聯絡人。

• 資料管理：資料是現代計算的命脈，但有效管理資料需要組織。排序演算法在資料管理中起著至關重要的作用。當您按名稱、日期或大小對文件清單進行排序時，您可以更輕鬆地找到所需的特定文件。此外，排序的資料有助於更快地檢索和分析，從而節省您的時間和精力。

• 資料庫最佳化：資料庫儲存大量訊息，從客戶記錄到金融交易。排序演算法顯著提高了資料庫查詢的效能。當您在電子商務資料庫中搜尋特定產品時，資料庫可能會根據您的搜尋條件（例如價格）對產品清單進行排序，以快速提供最相關的結果。

• 機器學習：機器學習演算法從資料中學習以進行預測或分類。然而，需要準備好資料才能進行有效的學習。排序演算法通常用於資料預處理步驟，以在將資料輸入機器學習模型之前組織和建構資料。這可以顯著提高學習過程的準確性和效率。

• 資料分析：資料分析就是從資訊中提取見解。排序演算法在這個過程中起著至關重要的作用。透過按各種屬性（例如日期、位置、客戶人口統計）對資料進行排序，您可以辨識在未排序的資料集中可能不易明顯的模式、趨勢和異常值。這使得資料分析師能夠更深入地了解資料，為金融、行銷和科學研究等各個領域的更好決策提供資訊。

• 作業系統：作業系統管理電腦的資源。排序演算法適用於各種作業系統任務。例如，排序演算法可用於確定 CPU 任務的優先權、有效管理記憶體分配或以目錄結構組織文件，從而確保電腦系統的平穩運作。

這些只是排序演算法如何滲透到我們日常生活中的幾個例子。

簡單解釋：

想像一下，你有一個雜亂的書架，裡面擺滿了各種主題的書。您想要按類型來組織它們（對它們進行排序）。以下是應用於此場景的排序演算法背後的主要概念和邏輯：

1. 比較：您一次拿兩本書，並根據它們的類型進行比較（就像比較清單中的兩個元素）。

2. 交換：如果類型不符合所需的順序（例如，歷史書放在小說之前），則交換它們在書架上的位置（就像重新排列清單中的元素一樣）。

3. 重複：您繼續一次比較和交換兩本書，直到所有書籍按類型按所需順序排列（清單中的所有元素都根據所選標準排序）。

排序演算法::

1. 冒泡排序

概念：冒泡排序是一種簡單的排序演算法，它迭代列表，反覆比較相鄰元素，如果順序錯誤則交換它們。想像氣泡上升到液體表面 - 具有較大值的元素每次通過都會「冒泡」到清單中。這個過程一直持續到不需要交換為止，這表示清單已排序。

解釋：

想像一下將一堆亂七八糟的玩具進行分類。冒泡排序的工作原理如下：

1. 進行多次遍歷：您多次瀏覽玩具清單。

2. 比較鄰居：在每一遍中，您將每個玩具與其鄰居進行比較。如果第一個玩具更大（或排序術語中的“更高”），則交換它們的位置。

3. 泡泡上升：每次交換時，較大的玩具（如泡泡）往往會移向清單的末端。

4. 繼續直到沒有交換：您在整個清單中重複這些比較和交換，直到完成一次完整的傳遞而無需交換。這表示列表已排序。

時間複雜度：不幸的是，在最壞情況和平均情況下，冒泡排序的時間複雜度都是 O(n^2)。這意味著排序時間隨著元素數量 (n) 的二次方增加。對於大型資料集，冒泡排序變得非常低效。

2.選擇排序

概念：選擇排序也遍歷列表，但它不是直接比較相鄰元素，而是專注於尋找未排序部分中的最小（或降序最大）元素。然後，該元素與未排序部分中的第一個元素交換，有效地將其放置在正確的排序位置。重複此過程，在每次通過時逐漸將未排序部分減少一個位置。

解釋：

想像一下根據身高安排學生拍照。選擇排序的工作原理如下：

1. 尋找最矮的（或最高的）：在每次遍歷中，您搜尋該行的整個未排序部分以尋找最矮的學生（或按降序排列最高的學生）。

2. 與第一個學生交換：一旦找到最矮的學生，就可以與未排序部分中的第一個學生交換他們的位置，有效地將他們放在行開頭的正確排序位置（最矮的在前面） 。

3. 重複並減少未排序部分：繼續此過程，將交換的元素視為已排序部分的開頭，並在剩餘的未排序部分中搜尋最小元素。

時間複雜度：與冒泡排序類似，選擇排序在平均情況和最壞情況下的時間複雜度均為 O(n^2)。這意味著排序時間隨元素數量呈二次方增長，從而導致大型資料集效率低下。

3.插入排序

概念：插入排序的工作原理是維護一個已排序的子列表，並迭代地將未排序部分中的元素插入到子列表中的正確位置。想像一下用塊建造一座塔，但您只能將它們一一加入，並且希望保持塔按高度排序。插入排序就像策略性地將每個新區塊放置在不斷增長的排序塔中的正確位置。

解釋：

想像一下按高度對書架上的書籍進行排序。插入排序的工作原理如下：

1. 從單一排序元素開始：從一個空的排序子清單開始（就像書架上只有一本書）。

2. 從未排序的部分中取出一個元素：您從未排序的堆中挑選一本書。

3. 移動與插入：您可以將新書與已排序子清單中的每本書進行比較，從右端開始。如果新書較短（或按降序排列較高），則可以移動現有書籍以騰出空間，並將新書插入到正確的位置以保持排序順序。

4. 重複並增長已排序的子清單：繼續此過程，從未排序的堆中獲取元素，將它們與已排序的子列表進行比較，並將它們插入到正確的已排序位置。這會逐漸增長排序的子列表，直到合併所有元素。

時間複雜度：插入排序適用於部分排序的資料。在一般情況下，對於已經排序的資料，它的時間複雜度為 O(n)，因此非常有效率。然而，對於完全隨機的資料（最壞情況），它可以回落到 O(n^2)，類似於冒泡排序和選擇排序。

4. 歸併排序

概念：合併排序採用巧妙的「分而治之」策略來有效地對清單進行排序。它將問題分解為更小、更易於管理的子問題，然後按排序順序將解決方案重新組合在一起。

解釋：

想像一下，你有一支龐大的軍隊，需要按照身高來組織。歸併排序的工作原理如下：

1. 劃分：將軍隊（列表）分成越來越小的組（子列表），直到每組只有一名士兵（元素）。這就像將一個大問題分解成更小、更容易解決的部分。

2. 征服：由於現在每個子清單只有一名士兵（元素），因此它已被視為「已排序」。這是分而治之方法的基本情況。

3. 合併：現在到了合併部分。您可以策略性地將已排序的子清單重新組合在一起，但以特定的方式。您比較每個子清單中的第一個士兵（元素），並將較短的士兵（較小的元素）放入最終的排序清單中。您不斷重複這種比較和放置，直到兩個子清單中的所有士兵（元素）都合併到最終的排序清單中。

4. 重複：您繼續遞歸地應用這種分而治之的策略，直到整個原始軍隊（列表）從最短到最高（最小到最大）排序。

時間複雜度：合併排序的美妙之處在於它的時間複雜度。在平均情況和最壞情況下，其複雜度為 O(n log n)。這意味著對清單進行排序所需的時間隨著元素數量(n) 呈對數增長，這比冒泡排序、選擇排序或插入排序（其複雜度為O(n^2)）要快得多。

5. 快速排序

概念：快速排序是另一種分而治之的排序演算法，但採用不同的方法。它依賴一個被稱為“樞軸”的策略性選擇元素來對列表進行分區並解決排序問題。

解釋：

想像一下，你的書架上堆滿了雜亂的書。快速排序的工作原理如下：

1. 選擇樞軸：您從書架中選擇一本書（樞軸）。可以透過不同的方式選擇該主元，但通常它是清單中的第一個或最後一個元素。

2. 分區：依樞軸重新排列書架上的書。類型按字母順序排列在樞軸類型之前的書籍位於一側，類型按字母順序排列在樞軸類型之後的書籍位於另一側。樞軸本身尚未放置。這種劃分有效地將較大的排序問題劃分為兩個較小的子問題。

3. 遞歸地征服：現在，您將兩個子清單（成堆的書）中的每一個都視為單獨的排序問題。您可以遞歸地將快速排序策略套用到這些子列表，為每個子列表選擇一個新的主元並相應地對它們進行分割。

4. 合併：兩個子清單排序後，將原始樞軸元素放置在兩個子清單之間正確的排序位置。現在，整個書架（清單）按字母順序排序。

時間複雜度：平均而言，快速排序的時間複雜度為 O(n log n)，這使得它對大型資料集非常有效率。然而，其性能可能會根據所選樞軸元件的不同而有所不同。選擇不當的主元（例如，總是排序或部分排序清單中的第一個或最後一個元素）可能會導致O(n^2) 的最壞情況，類似於冒泡排序、選擇排序和插入排序。

3.樹的遍歷演算法：

什麼是樹遍歷？

樹遍歷是指探索樹資料結構的系統方法。這就像有一個路線圖可以精確地存取鄰裡（樹）中的每個房屋（節點）一次，確保您不會迷路或重新存取同一棟房屋。與可以直接按位置存取元素的簡單資料結構不同，樹需要特定的演算法來導航節點之間的連接。這些遍歷演算法定義了存取每個節點的順序，可讓您對它們包含的資料執行操作，例如搜尋特定值、新增節點或刪除現有節點。遍歷技術有多種，每種技術都有其優點和應用，這使得樹遍歷成為電腦科學中的基本概念。

介紹

樹遍歷，也稱為樹搜尋，是在僅包含樹邊的圖上執行的演算法，該演算法僅存取每個節點一次。此類別中的演算法僅在存取每個節點的順序上有所不同。遍歷樹的兩種經典方法是廣度優先搜尋（bfs），即在進入下一層之前存取同一級別或距根部距離的節點；深度優先搜尋，其中分支中的所有節點或從根到葉的一組路徑在傳遞到下一個分支之前都會被存取。還有其他方法，它們使用啟發式或隨機採樣在樹中移動來加速該過程。

概括：

• 目的：系統探索樹資料結構，確保每個節點僅被存取一次。

• 優點：支援搜尋特定資料、插入新節點或刪除現有節點等操作。

• 主要區別：演算法分為兩種主要方法：

* **Breadth-First Search (BFS):** Visits nodes level by level, starting from the root and progressing outward.

* **Depth-First Search (DFS):** Explores one branch (path) as far as possible before backtracking and exploring another branch. Further variations of DFS exist for specific applications.

• 其他技術：其他方法利用啟發式或隨機取樣來加快遍歷速度。

術語：

1. 樹：一種分層資料結構，模擬顛倒的樹，其節點（資料點）透過邊（連結）連接。節點可以有零個或多個子節點，形成分支，並最終導致底部的葉節點（沒有子節點的節點）。

2. 節點：樹的基本建構塊，包含資料和對其子節點的潛在引用。想像一下附近的一棟房子——它保存資訊（資料）並透過道路（邊緣）連接到其他房子（子節點）。

3.根節點：樹中最頂層的節點，作為遍歷演算法的起點。將其視為附近的主屋，從這裡開始探索。

4.葉子節點：沒有子節點的節點，代表樹中分支的「末端」。想像位於社區邊緣的房屋，沒有進一步的聯繫。

5.邊：樹中兩個節點之間的連接，描述它們之間的關係。想想連接附近房屋的道路。

6. 遍歷：僅存取樹中每個節點一次的系統過程。這就像探索整個社區，確保您參觀每棟房屋而不會錯過任何一棟或重新參觀同一棟房屋。

7.廣度優先搜尋（BFS）：一種從根開始向外逐階存取節點的遍歷方法。想像一下，透過造訪第一條街道（層）上的所有房屋，然後再前往下一條街道（層）上的房屋來探索社區。

8.深度優先搜尋（DFS）：一種遍歷方法，在回溯和探索另一個分支之前，先沿著一個分支（路徑）探索盡可能遠的地方。想像一下，沿著一條路（分支）探索附近區域，直到到達死胡同（葉節點），然後回溯並嘗試另一條路。 DFS 的常見變體包括前序、中序和後序，每種形式都有存取分支內節點的特定順序。

樹遍歷演算法的特點：

1. 只存取每個節點一次：

• 樹遍歷的核心原則是保證樹中的每個節點都被恰好存取一次。這可以防止冗餘處理並確保對樹結構的完整探索。

2. 探訪順序：

• 雖然每個節點僅被存取一次，但樹遍歷演算法的定義特徵在於它們存取節點的順序。不同的演算法會優先考慮以特定順序探索節點，從而產生不同的遍歷模式。

3. 遞歸與迭代實作：

• 樹遍歷演算法可以遞歸或迭代地實現。遞歸方法涉及定義在子樹上呼叫自身的函數，模仿樹的層次結構性質。迭代方法利用迴圈和堆疊來管理遍歷過程。

4.時間與空間複雜度：

• 與任何演算法一樣，樹遍歷方法具有相關的時間和空間複雜度。時間複雜度是指基於樹中節點數 (n) 執行演算法所需的時間量。常見的複雜度包括 O(n)（線性）和 O(n log n)（對數），BFS 和 DFS 變體根據實現的不同具有不同的複雜度。空間複雜度反映了演算法執行所需的額外記憶體量，通常取決於用於遍歷的資料結構（例如堆疊）。

5.特定於應用的選擇：

• 樹遍歷演算法的選擇在很大程度上取決於手頭上的具體任務。例如，BFS 可能更適合尋找樹中兩個節點之間的最短路徑，而具有變體的 DFS 可用於搜尋特定資料或探索所有可能的路徑。

6. 不可修改：

• 一般來說，樹遍歷演算法旨在探索現有的樹結構，而不修改樹本身。它們存取節點，對它們包含的資料執行操作，但通常不會更改樹中的連接或資料。

樹遍歷演算法的應用：

1. 檔案系統導航：

• 作業系統使用樹遍歷演算法來導航電腦上的目錄結構。將您的檔案系統想像成一棵樹，其中資料夾作為節點，子資料夾和檔案作為子節點。廣度優先搜尋 (BFS) 可用於列出目錄及其子目錄中的所有文件，而深度優先搜尋 (DFS) 可用於在層次結構中定位特定文件。

2. 網頁抓取：

• 像 Google 這樣的搜尋引擎利用 BFS 或 DFS 變體來抓取網路。他們從種子 URL（根節點）開始，有系統地探索連結的網頁（子節點）。 BFS 確保在進入更深層次之前探索特定層級（網站）的所有頁面，而 DFS 可能會在回溯和探索其他網站之前更深入地研究特定網站。

3.人工智慧（AI）：

• 人工智慧中的遊戲演算法通常使用樹遍歷來探索可能的動作及其結果。將西洋棋遊戲想像成一棵樹，當前棋盤狀態作為根節點，潛在的移動作為通往新棋盤狀態（子節點）的分支。具有修剪技術的深度優先搜尋可用於評估潛在的移動並確定最有希望的策略。

4.社會網絡分析：

• 社群媒體平台利用樹遍歷來推薦聯繫或探索朋友網路。將您的個人資料想像為一個節點，將朋友作為子節點。遍歷演算法可用於建議基於共同朋友（樹中的共同祖先）的連接或探索網路以了解資訊流或影響力。

5.電腦圖形學：

• 光線追蹤是一種用於在 3D 圖形中實現逼真光照效果的技術，通常採用樹遍歷演算法。虛擬場景可以表示為一棵樹，其中物件作為節點，它們的空間關係作為邊緣。遍歷有助於確定光線與哪些物件交互，從而建立逼真的陰影和反射。

6. 網路路由：

• 電腦網路中的路由協定使用樹遍歷的變體來找到資料包到達目的地的最佳路徑。將網路想像成一棵樹，路由器作為節點，連接作為邊緣。遍歷演算法有助於確定資料在網路中不同點之間傳輸的最有效路徑。

簡單解釋：

想像一下，您是一名送貨員，您有一堆包裹要在附近送貨。附近的房屋透過道路連接起來，形成樹狀結構。

• 房屋是節點：每個房屋代表樹中的一個節點，包含地址（資料）等資訊以及可能由道路（邊）連接的相鄰房屋（子節點）的地址。

• 您的遞送路線就是遍歷：樹遍歷演算法定義您存取每個房屋（節點）以遞送包裹（對資料執行操作）的順序。

您可以透過兩種主要方式進行交付，這對應於兩種常見的樹遍歷方法：

1. 廣度優先搜尋（BFS）：像一個不斷擴大的圓圈一樣提供：

• 您從清單中的第一個房子（根節點）開始。

• 您將包裹運送到該房屋，然後存取同一條街道（層）上與其直接相連的所有房屋（鄰居/子節點），然後繼續前進。

• 一旦您運送到第一條街道（層）上的所有房屋，您就會移動到下一條街道（層）並重複該過程，在前往下一層之前存取該層上的所有房屋。

這就像一個不斷擴大的圓圈——您從中心（根部）開始，逐漸向外工作，確保在移動到下一個之前，您可以運送到街道（層）上的所有房屋。如果您想先優先考慮向附近區域的所有房屋送貨，這種方法很有用，也許是因為它們都在同一個街區，並且最大限度地減少行程時間很重要。

2. 深度優先搜尋（DFS）：深入研究一條街道：

• 您從清單中的第一棟房子（根節點）開始。

• 您將包裹運送到該房屋，然後選擇一條從該房屋引出的相連道路（分支），並沿著它一直走到終點（葉節點） ，在原路返回之前運送到該路徑（分支）上的所有房屋。

• 一旦到達該路的盡頭（分支），您就回溯到最後一個路口（父節點）並選擇另一條路（分支）進行探索，將物品運送到該新路徑上的所有房屋，直到到達另一個死胡同（葉節點） 。

這就像探索迷宮一樣——你選擇一條路徑（分支）並沿著它一路走下去，運送到沿途的房屋，直到你到達死胡同（葉節點）。然後你原路返回並嘗試另一條路徑（分支），直到你到達所有房屋。如果您正在快速查找特定地址並希望在前往另一條街道（分支）之前探索整條街道（分支），則此方法可能會很有用。

演算法類型：

1.廣度優先搜尋（BFS）：

• 概念： BFS逐級存取節點，從根節點開始，逐層向外進行。想像一下探索一個家譜； BFS 將在向下移動到其子節點（下一層）之前存取所有兄弟節點（同一層級的節點）。

• 怎麼運作的：

1. Start at the root node and add it to a queue (a data structure that follows a "first-in, first-out" principle).

2. Remove the first node from the queue and visit it (process its data).

3. Add all the unvisited child nodes of the removed node to the back of the queue.

4. Repeat steps 2 and 3 until the queue is empty.

• 例子：

考慮一棵簡單的樹：

      A
     / \
    B   C
   / \ / \
  D  E F  G

BFS 遍歷將依下列順序存取節點：A、B、C、D、E、F、G。

2.深度優先搜尋（DFS）：

• 概念： DFS 沿著一個分支（路徑）探索盡可能遠的距離，然後回溯並探索另一個分支。 DFS 還有更多變體，但這裡我們將重點放在基本方法上。

• 怎麼運作的：

1. Start at the root node.

2. Visit the node (process its data).

3. If there are any unvisited child nodes, choose one and repeat steps 2 and 3, essentially following that branch (path) until you reach a leaf node (a node with no children).

4. Once you reach a leaf node, backtrack to the parent node and repeat step 3, exploring another unvisited child node (if any) of the parent.

5. Continue backtracking and exploring until all nodes have been visited.

• 例子：

使用與之前相同的樹：

      A
     / \
    B   C
   / \ / \
  D  E F  G

DFS 遍歷可以以各種順序存取節點，具體取決於每一步選擇的子節點。可能的順序是：A、B、D、E、C、F、G。

主要區別：

• BFS強調逐級存取節點，確保在深入之前先進行更廣泛的探索。

• DFS 優先考慮完全探索一個分支（路徑），然後再轉向另一個分支（路徑），可能會更快到達特定節點，但不能保證逐級存取。

結論 ：

總而言之，這個基本演算法之旅為您理解基本的搜尋、排序和樹遍歷技術奠定了堅實的基礎。這些解釋使用了清晰的語言和相關的類比，使這些抽象概念更加平易近人、直觀。無論您是經驗豐富的程式設計師還是剛開始涉足電腦科學，這種理解都為建立高效且有效的程式奠定了基石。

隨著您對知識的渴望與日俱增，請更深入研究！我的儲存庫充滿了各種演算法和資料結構，等待您的探索（演算法-資料-結構）。這是一個寶庫，您可以在這裡進行實驗、練習並鞏固您對這些基本建置模組的掌握。

雖然某些部分仍在建設中，反映了我自己正在進行的學習旅程（這個旅程可能需要 2-3 年才能完成！），但儲存庫正在不斷發展。

冒險不止於探索！我非常重視您的反饋。在文章中遇到障礙？有建設性的批評要分享嗎？還是只是想引發一場關於演算法的對話？我的門（或者更確切地說，我的收件匣）總是開著的。在 Twitter 上聯絡： @m__mdy__m或 Telegram：@m_mdy_m。此外，我的 GitHub 帳戶m-mdy-m歡迎討論和貢獻。讓我們共同建立一個充滿活力的學習社區，在這裡我們分享知識並突破我們的理解界限。

原文出處：https://dev.to/m__mdy__m/basic-algorithms-5bep