🔧 阿川の電商水電行

Shopify 顧問、維護與客製化

💡

小任務 / 單次支援方案

單次處理 Shopify 修正／微調

⭐️

維護方案

每月 Shopify 技術支援 + 小修改 + 諮詢

🚀

專案建置

Shopify 功能導入、培訓 + 分階段交付

👉 瞭解詳情 / 免費諮詢

小編精選 - 技術文章翻譯 · 11月11日

關於截至2025年11月全球最快收聽率計算演算法的開發與實施

結論 - 2025年11月時點的世界最快向聽數計算演算法實作

本稿所介紹的向聽數計算演算法的實作已公開於 https://github.com/Cryolite/nyanten。此實作在計算每一手牌的向聽數時，在使用 Intel Core i9-12900、Ubuntu 24.04.3 LTS、GCC 15.2.0 的環境下，測得的平均速度約為 40 奈秒。如果對於 2025年11月時點的世界最快向聽數計算演算法的實作有異議，請攜帶更高速的實作與筆者聯繫。

向聽數 - 本文章所提議的演算法計算的內容

向聽數是麻將中顯示手牌進展的指標之一，定義為「聽牌所需的最小摸牌次數」。因此，向聽數計算演算法的輸入為 2 張、5 張、8 張、11 張、14 張的麻將牌的集合（在摸牌之後的情況），或是 1 張、4 張、7 張、10 張、13 張的麻將牌的集合（在非摸牌之後的情況），並將每個輸入視為手牌，輸出所需的最小摸牌次數直到聽牌為止。

和了形可大致分為 4 面子 1 雀頭形（實際上是考慮副露的 $n$ 面子 1 雀頭形，$n \in { 0, 1, 2, 3, 4}$）、七對子形、國士無雙形。在這其中，針對七對子形及國士無雙形的向聽數計算較為容易，因此本稿不再闡述。以下將著重於針對 4 面子 1 雀頭形的向聽數計算進行說明。

在社會上，常常會提及到針對 4 面子 1 雀頭形的向聽數「定義」為

$$\text{向聽數} = 8 - \text{面子的數量} \times 2 - \text{面子候補的數量}$$

其中

$$\text{面子的數量} = \text{順子的數量}+\text{刻子的數量}+\text{副露的數量}$$

$$\text{面子候補的數量} = \text{塔子的數量} + \text{對子的數量}$$

此計算公式在近似計算「聽牌所需的最小摸牌次數」方面相當優秀，尤其在人的計算下非常有效，但實際上並未正確計算「聽牌所需的最小摸牌次數」。可能的 $n$ 面子 1 雀頭形手牌的型態有 4250305029168216000 種，其中 263674494 種手牌對應此計算公式會產生錯誤的數值。[^1][^2] 在民間廣泛流傳的「向聽數計算演算法」中，有一部分基於此計算公式（或其變種）[^3][^4]，如此便形成了錯誤的演算法（好聽點是近似計算的演算法）。進一步來說，基於上述計算公式的「向聽數計算演算法」，在速度上與數理上正確定義的向聽數相關的算法（例如 https://github.com/tomohxx/shanten-number 或本稿所提議的算法）相比並無任何優勢。因此，以上述計算公式為基礎的「向聽數計算演算法」在當今的現實中並沒有被採用的正當理由，只是過去的遺物而已。

若無法採用上述「向聽數的定義」，那麼向聽數究竟是什麼（數理上說，向聽數的定義是什麼）便成了問題。結論是，給定的手牌的向聽數，是在列舉所有可能的聽牌形後，所需的最小摸牌次數計算出來的其中最小的值。

然而，這個向聽數的定義存在一個問題。依據這個定義，聽牌形及和了形的向聽數皆為0，導致無法區分聽牌形與和了形。因此，這裡需要給出一個擴展的向聽數定義，使得對於聽牌形的向聽數為0，而對於和了形的向聽數為-1。為此，重新引入一個「置換數」的數值。某手牌的置換數是列舉所有可能的和了形後，對於每一和了形計算所需的最小摸牌次數中的最小值。根據此定義，當某手牌為和了形時，其置換數為0；當為聽牌形時，置換數為1；一般地，若非和了形，則置換數將比向聽數大1。

以下接下來將著重於計算向聽數的替代，即置換數。

例如，

對於這手牌的置換數（向聽數），依據定義進行計算會得出什麼結果呢？首先列舉所有可能的 4 面子 1 雀頭形和了形 12859078207674 種，從中找出最小摸牌次數可以達到的形。最終，從中找到的一個和了形是

從該手牌轉換到此和了形所需的最小摸牌次數為2，因此該手牌的置換數為2（向聽數為1）。

上述是針對13張或14張的手牌所進行的置換數（向聽數）計算步驟，但實際上需要考慮副露的情況。故當輸入的手牌為1張或2張時，將列舉出所有 0 面子 1 雀頭的和了形，並從中找出需要的最小摸牌次數。以下同理，當輸入的手牌為4張或5張時，則需列舉所有 1 面子 1 雀頭的和了形，並找出需要的最小摸牌次數。同理，當輸入的手牌為7張或8張時，需列舉所有 2 面子 1 雀頭的和了形；若手牌為10張或11張時，則需列舉所有 3 面子 1 雀頭的和了形。

部分向聽數

在上述例子中，類似地針對13張或14張的置換數（向聽數）計算步驟提到需要列舉所有可能的 4 面子 1 雀頭形和了形 12859078207674 種。然而，依據定義進行此操作會在計算上變得非常緩慢。因此，藉由利用麻將的規則，更快速地計算向聽數。

要構成 4 面子 1 雀頭時，例如，可以使用萬子構成1面子0雀頭，筒子構成0面子0雀頭，索子構成2面子1雀頭，字牌則構成1面子0雀頭。一般來說，若萬子中有 $m_0$ 面子 $h_0$ 雀頭，筒子中有 $m_1$ 面子 $h_1$ 雀頭，索子中有 $m_2$ 面子 $h_2$ 雀頭，字牌中有 $m_3$ 面子 $h_3$ 雀頭，那麼整體手牌必須滿足 $m_0 + m_1 + m_2 + m_3 = 4$ 及 $h_0 + h_1 + h_2 + h_3 = 1$。所有這些組合的列舉請參見此 https://gist.github.com/Cryolite/29f64c49b198c17202ab74ff8a527ca7。同樣地，要構成 3 面子 1 雀頭的整體，就需要得到 $m_0 + m_1 + m_2 + m_3 = 3$ 及 $h_0 + h_1 + h_2 + h_3 = 1$ 的組合，相關組合可參見 https://gist.github.com/Cryolite/af18778dbe9dc5fbfbe25c83696caa8a。而要構成 2 面子 1 雀頭需滿足 $m_0 + m_1 + m_2 + m_3 = 2$ 及 $h_0 + h_1 + h_2 + h_3 = 1$，參見 https://gist.github.com/Cryolite/80a0204e0568983bd300ccc461b78246。要達成 1 面子 1 雀頭則滿足 $m_0 + m_1 + m_2 + m_3 = 1$ 及 $h_0 + h_1 + h_2 + h_3 = 1$的組合，相關的可參見 https://gist.github.com/Cryolite/fa561f977d5197c8c824113136d721bc。若要達成 0 面子 1 雀頭，則需滿足 $m_0 + m_1 + m_2 + m_3 = 0$ 及 $h_0 + h_1 + h_2 + h_3 = 1$ 的組合，參見 https://gist.github.com/Cryolite/3633cc5e8a26bef257dc0fd281bc8d10。

根據上述分析，當計算例如

這手牌的向聽數時，便需著重於：

萬子構成 0 面子 0 雀頭，筒子構成 0 面子 0 雀頭，索子構成 0 面子 0 雀頭，字牌則構成 4 面子 1 雀頭所需的最小摸牌次數
萬子構成 0 面子 0 雀頭，筒子構成 0 面子 0 雀頭，索子構成 0 面子 1 雀頭，字牌構成 4 面子 0 雀頭所需的最小摸牌次數
萬子構成 0 面子 0 雀頭，筒子構成 0 面子 0 雀頭，索子構成 1 面子 0 雀頭，字牌構成 3 面子 1 雀頭所需的最小摸牌次數
......

如上，對於每一種情形 https://gist.github.com/Cryolite/29f64c49b198c17202ab74ff8a527ca7 中列舉的所有情況計算所需的最小摸牌次數，最小的數值即為置換數。

因此在向聽數計算過程中，需要注意到首先針對手牌的萬子部分

萬子部分構成 0 面子 0 雀頭所需的最小摸牌次數
萬子部分構成 1 面子 0 雀頭所需的最小摸牌次數
萬子部分構成 2 面子 0 雀頭所需的最小摸牌次數
萬子部分構成 3 面子 0 雀頭所需的最小摸牌次數
萬子部分構成 4 面子 0 雀頭所需的最小摸牌次數
萬子部分構成 0 面子 1 雀頭所需的最小摸牌次數
萬子部分構成 1 面子 1 雀頭所需的最小摸牌次數
萬子部分構成 2 面子 1 雀頭所需的最小摸牌次數
萬子部分構成 3 面子 1 雀頭所需的最小摸牌次數
萬子部分構成 4 面子 1 雀頭所需的最小摸牌次數

同樣的，依次針對手牌的筒子部分、索子部分與字牌部分計算相應的值。

因此，要計算某手牌的置換數（向聽數），只需關注該手牌的每種牌型（萬子、筒子、索子、字牌）部分，計算出該部分中構成 $m$ 面子 $h$ 雀頭（$m \in { 0, 1, 2, 3, 4},$ $h \in { 0, 1}$）所需的最小摸牌次數，然後只需結合這些計算出的數值，便可得出該手牌的整體置換數（向聽數）。若有某手牌被給定時，針對該手牌的某牌色部分並重點計算所需的最小摸牌次數，稱之為（針對該顏色的 $m$ 面子 $h$ 雀頭的）部分置換數。

例如，對於手牌

對萬子而言：

萬子中 $0$ 面子 $0$ 雀頭的部分置換數為 $0$
萬子中 $1$ 面子 $0$ 雀頭的部分置換數為 $0$
萬子中 $2$ 面子 $0$ 雀頭的部分置換數為 $1$
萬子中 $3$ 面子 $0$ 雀頭的部分置換數為 $4$
萬子中 $4$ 面子 $0$ 雀頭的部分置換數為 $7$
萬子中 $0$ 面子 $1$ 雀頭的部分置換數為 $1$
萬子中 $1$ 面子 $1$ 雀頭的部分置換數為 $1$
萬子中 $2$ 面子 $1$ 雀頭的部分置換數為 $3$
萬子中 $3$ 面子 $1$ 雀頭的部分置換數為 $6$
萬子中 $4$ 面子 $1$ 雀頭的部分置換數為 $9$

如此類推，當某手牌被給定時，其各色部分的部分置換數

$0$ 面子 $0$ 雀頭的部分置換數
$1$ 面子 $0$ 雀頭的部分置換數
$2$ 面子 $0$ 雀頭的部分置換數
$3$ 面子 $0$ 雀頭的部分置換數
$4$ 面子 $0$ 雀頭的部分置換數
$0$ 面子 $1$ 雀頭的部分置換數
$1$ 面子 $1$ 雀頭的部分置換數
$2$ 面子 $1$ 雀頭的部分置換數
$3$ 面子 $1$ 雀頭的部分置換數
$4$ 面子 $1$ 雀頭的部分置換數

可以整齊排列成一列，稱之為該手牌的（針對該色）部分置換數列。

例如，對於手牌

對筒子的部分置換數列表示為 $(0, 1, 2, 5, 8, 0, 1, 4, 7, 10)$。

動態規劃實現置換數（向聽數）的快速計算

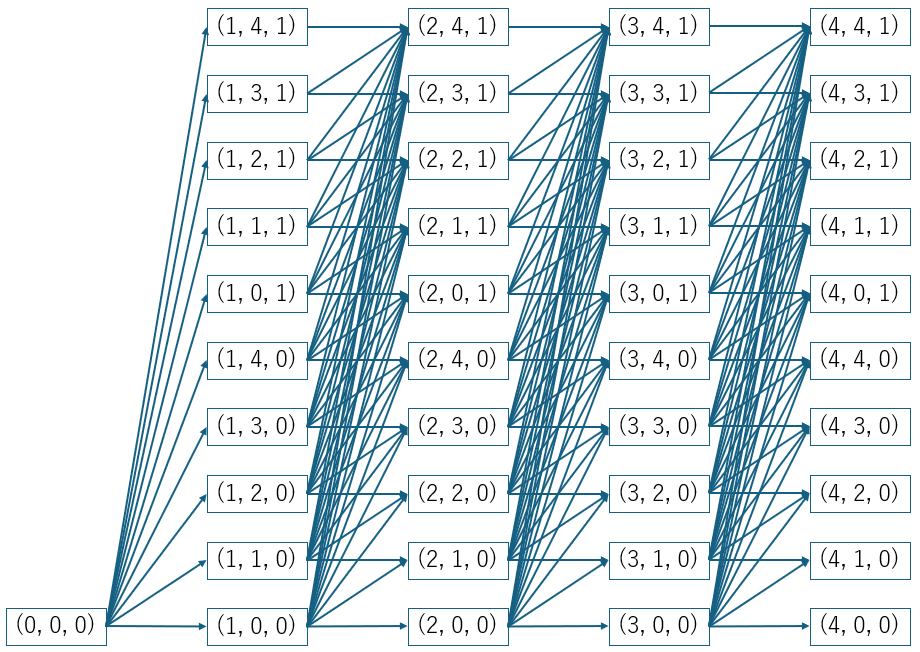
當某手牌被給定時，若其每種顏色的部分置換數列可提前計算，則最終的置換數（向聽數）可利用動態規劃快速計算。在計算整體手牌的 $m$ 面子 1 雀頭的置換數（向聽數）時，此動態規劃可視為在以下有向無環圖中尋找從節點 $(0, 0, 0)$ 到節點 $(4, m, 1)$ 的最小成本路徑之問題。

此處，

從節點 $(0, 0, 0)$ 到節點 $(1, m, h)$ 的邊的成本為萬子中 $m$ 面子 $h$ 雀頭對應的部分置換數
從節點 $(1, m, h)$ 到節點 $(2, m', h')$ 的邊的成本為筒子中 $m' - m$ 面子 $h' - h$ 雀頭對應的部分置換數
從節點 $(2, m, h)$ 到節點 $(3, m', h')$ 的邊的成本為索子中 $m' - m$ 面子 $h' - h$ 雀頭對應的部分置換數
從節點 $(3, m, h)$ 到節點 $(4, m', h')$ 的邊的成本為字牌中 $m' - m$ 面子 $h' - h$ 雀頭對應的部分置換數

最小完全哈希函數的部分置換數列預計算

根據上述的說明，給定某手牌，以計算其置換數（向聽數），需計算該手牌的

萬子中的部分置換數列
筒子中的部分置換數列
索子中的部分置換數列
字牌中的部分置換數列

並最終將這些數列結合起來。而由於對於某手牌各色的部分置換數列的計算速度非常緩慢，因此決定導入事先計算部分置換數列的想法。也就是將數牌從0張到14張的901035種所有的型態，以及字牌從0張到14張的43130種型態，事先計算各別的部分置換數列。

預先計算的部分置換數列會以數牌或字牌的型態為鍵，並將對應於每一鍵的部分置換數列儲存於某種資料結構中。而採用何種資料結構即為問題所在。本稿所介紹的將使用包含最小完全哈希函數的數組作為此資料結構。

首先是鍵，數牌的情況下為 $0, 1, 2, 3, 4$ 的任意9位數字排列且數字總和不超過14；在字牌的情況下為 $0, 1, 2, 3, 4$ 的任意7位數字排列且數字總和不超過14，這一點是顯而易見的。

針對這類鍵，簡單的方式包括：

使用普通的哈希函數的哈希表
將鍵看作是5進數的自然數表達來計算數組的索引

但前者的效率受限於哈希函數的速度，且由於哈希衝突的原因，必須將鍵在哈希表中儲存；後者將忽視「數字總和不超過14」的約定，可能導致數組的大小過於龐大。

本稿所介紹的想法是在 $0, 1, 2, 3, 4$ 的數字排列且數字總和不超過14的情況下，給每一種型態按照字典序編號。換句話說，對於這類排列，使用最小完全哈希函數。

此最小完全哈希函數的詳盡說明可參考：

因此，部分置換數列所使用的資料結構將會是針對數牌的大小為 405350 的數組，針對字牌的大小為 43130 的數組。

部分置換數列的差分壓縮

（本節的基本想法是由 tomohxx 提出的。）

預先計算的部分置換數列簡單來說，即為 $0$ 到 $9$ 的任何數字排列共10個（最大為 $9$ 是因為 $4$ 面子 $1$ 雀頭形的置換數最大為 $9$（向聽數的最大為 $8$）），但透過編碼的巧妙設計，可壓縮實際的大小。

首先，$0$ 面子 $0$ 雀頭的部分置換數始終為 $0$，因此無需記錄。此外，我們將記錄如下數值，而非直接記錄部分置換數列：

$1 \text{面子} 0 \text{雀頭的部分置換數}$
$(2 \text{面子} 0 \text{雀頭的部分置換數}) - (1 \text{面子} 0 \text{雀頭的部分置換數})$
$(3 \text{面子} 0 \text{雀頭的部分置換數}) - (2 \text{面子} 0 \text{雀頭的部分置換數})$
$(4 \text{面子} 0 \text{雀頭的部分置換數}) - (3 \text{面子} 0 \text{雀頭的部分置換數})$
$0 \text{面子} 1 \text{雀頭的部分置換數}$
$(1 \text{面子} 1 \text{雀頭的部分置換數}) - (1 \text{面子} 0 \text{雀頭的部分置換數})$
$(2 \text{面子} 1 \text{雀頭的部分置換數}) - (2 \text{面子} 0 \text{雀頭的部分置換數})$
$(3 \text{面子} 1 \text{雀頭的部分置換數}) - (3 \text{面子} 0 \text{雀頭的部分置換數})$
$(4 \text{面子} 1 \text{雀頭的部分置換數}) - (4 \text{面子} 0 \text{雀頭的部分置換數})$

1至4理論上不會超過 $3$ 的數；而5至9則理論上不會超過 $2$ 的數。因此，上述8個數字可以被編碼為 $\log_2(4^4 \times 3^5) = \log_2 62208 = 15.924...$ 位，並可存放為16位的整數。當然，可以使用1至9的數值，來完全解碼回原來的部分置換數列。

根據這一想法壓縮的部分置換數列，以下將稱之為部分置換數列的差分壓縮碼。