🔧 阿川の電商水電行

Sapeet 的 SWE 渡邊。
最近我與公司內的成員熱衷於 ARC Raiders。
我也想自己製作一個自製的 ARC(機械生命體),因此對人工生命(Artificial Life)產生了興趣()。
為什麼現在是 ALIFE
ALIFE(Artificial Life 的縮寫)是一個旨在人工再現生命系統的領域。
特別是進化的再現(如突變)和模式創發等研究非常著名。
例子)
- 演化健身房(Evolution Gym):模擬虛擬生物的進化研究
- L 系統(L-system):模擬植物結構的研究
 (圖片來源:維基百科)
(圖片來源:維基百科)
若能最終再現人類等複雜的生命系統,將可幫助解決疾病等問題,是一門有前景的研究領域。
AI 與 ALIFE
大體而言,AI 是針對目的進行優化(自上而下的方法),而 ALIFE 則是交由偶發性進化(自下而上的方法)來主導。
在實體 AI 的現場,應用人類所創造演算法的方法正在增多,尤其是從在模擬環境中成長的方法(Sim2Real)。
嘗試 ALIFE
① 生命遊戲(Conway's Game of Life,1970 年)
數學家約翰·霍頓·康威發明的細胞自動機。
(※細胞自動機 = 以網格排列的「細胞」根據簡單的「規則」隨時間變化自身的狀態(顏色或數值等)的一個離散計算模型)
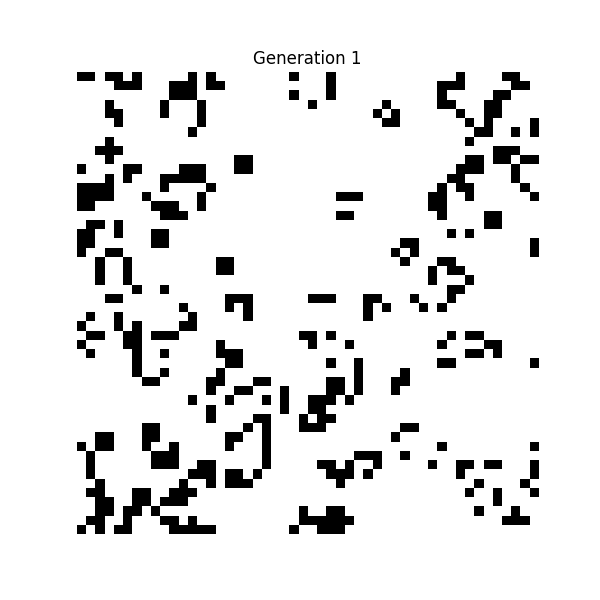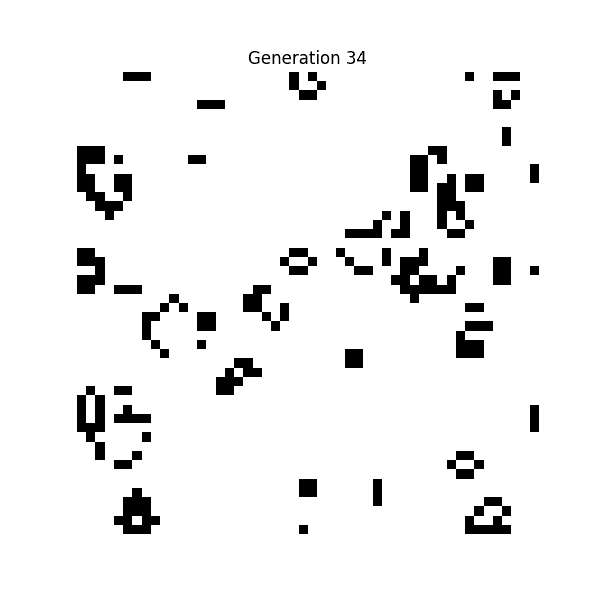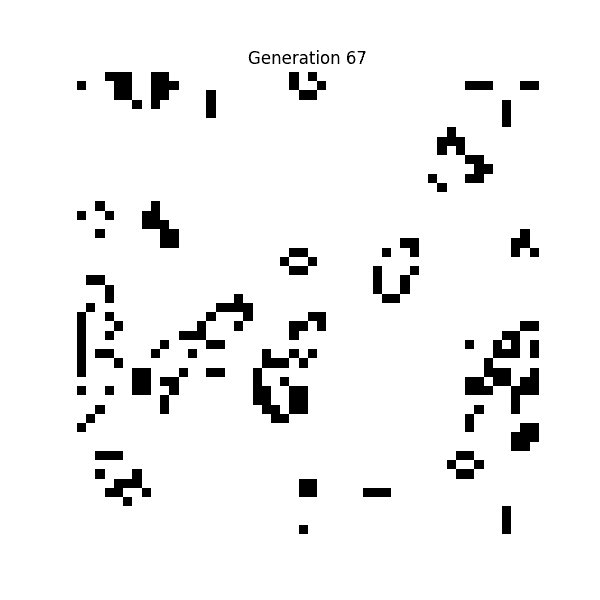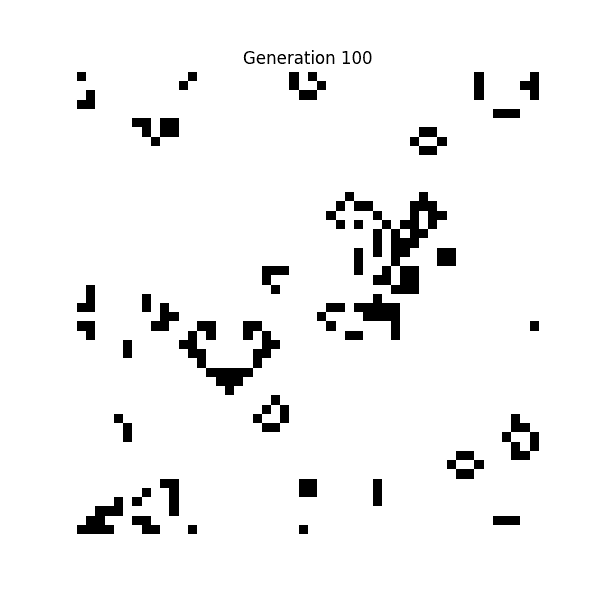
這是一個模擬白黑點根據「過疎則死」「適度則增」的極簡規則運行的簡單模擬,但這成為了人工生命研究的起點。
生命遊戲的規則
- 誕生:若周圍剛好有 3 個存活的細胞,死亡的細胞將在下一代重生
- 生存:若周圍有 2 或 3 個存活的細胞,存活細胞在下一代也會繼續存在
- 過疎:若周圍只有 1 個或更少的存活細胞,則因孤獨而死亡
- 過密:若周圍有 4 個或更多的存活細胞,則因過密而死亡
嘗試生命遊戲
💡 可以確認從簡單的規則中產生複雜的模式。有些模式會立即消失,有些則會持久存在。
<details>
<summary>Python 程式碼</summary>
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
from IPython.display import HTML
def game_of_life(size=50, steps=100):
# 產生隨機初始狀態
grid = np.random.choice([0, 1], size=(size, size), p=[0.8, 0.2])
fig, ax = plt.subplots(figsize=(6, 6))
img = ax.imshow(grid, cmap='binary')
ax.set_title('Conway\'s Game of Life')
ax.axis('off')
def update(frame):
nonlocal grid
# 計算鄰近細胞數量
neighbors = sum(
np.roll(np.roll(grid, i, 0), j, 1)
for i in (-1, 0, 1) for j in (-1, 0, 1)
if (i != 0 or j != 0)
)
# 套用規則
grid = ((grid == 1) & (neighbors >= 2) & (neighbors <= 3)) | \
((grid == 0) & (neighbors == 3))
grid = grid.astype(int)
img.set_array(grid)
ax.set_title(f'Conway\'s Game of Life - Generation {frame + 1}')
return [img]
anim = FuncAnimation(fig, update, frames=steps, interval=100, blit=True)
plt.close() # 防止靜態圖片顯示
return HTML(anim.to_jshtml())
# 執行
game_of_life(size=50, steps=100)</details>
② Boids(1986 年)
由克雷格·雷諾茲開發的模擬群體行為的演算法。
"Boids" 是 "bird-oid object"(鳥形物件)的縮寫。
Boids 的規則
- 分離:保持與附近的同伴有一定距離,以避免碰撞
- 整列:儘可能與附近的同伴保持相同的方向
- 結合:盡量向群體的中心移動
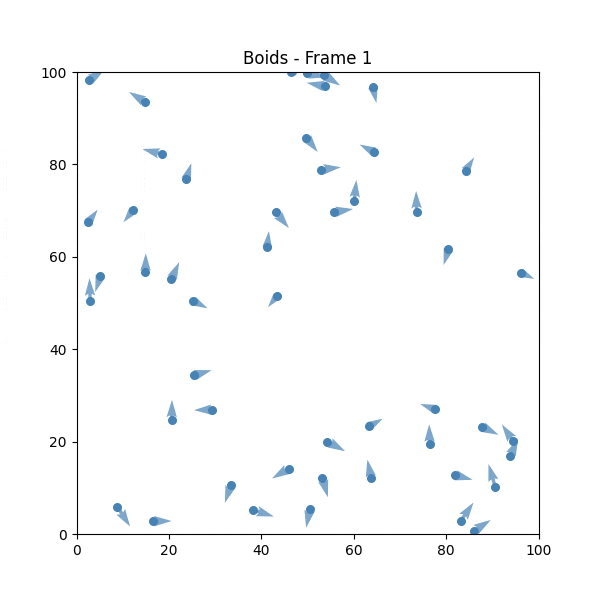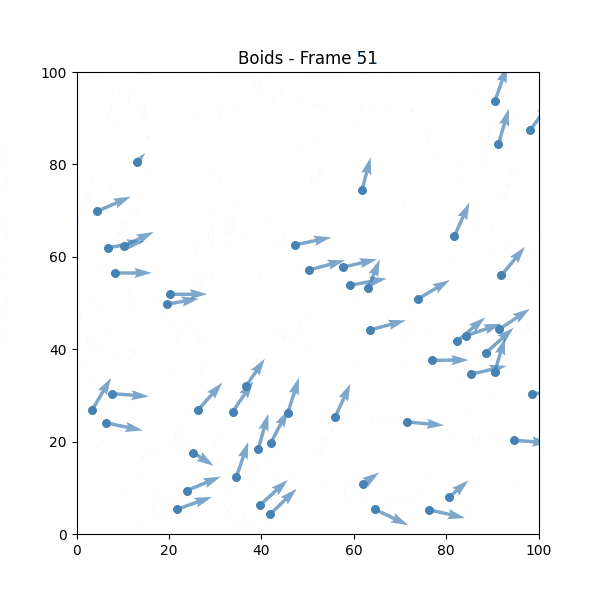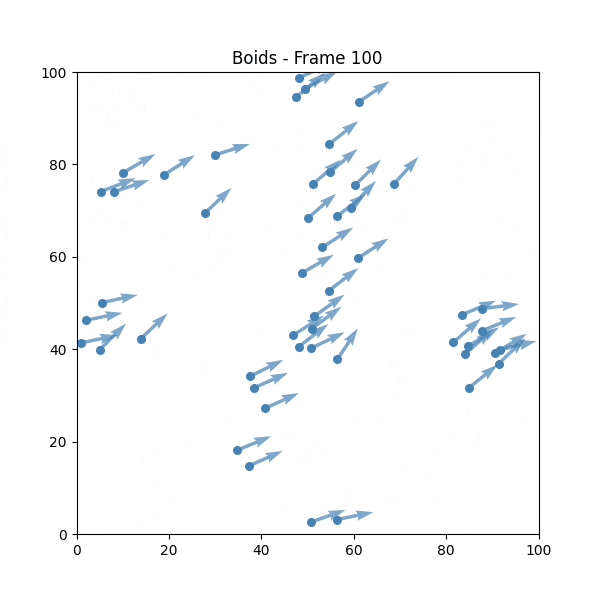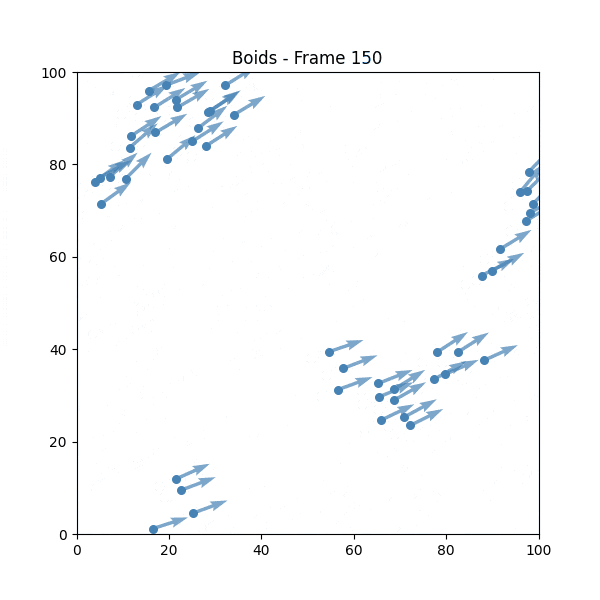
嘗試 Boids
💡 雖然規則簡單,但可以明確看到從個別的隨機行動中產生群體行為。
<details>
<summary>Python 程式碼</summary>
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
from IPython.display import HTML
class Boid:
def __init__(self, x, y):
self.position = np.array([x, y], dtype=float)
angle = np.random.uniform(0, 2 * np.pi)
self.velocity = np.array([np.cos(angle), np.sin(angle)]) * 2
def boids_simulation(num_boids=50, steps=200):
width, height = 100, 100
# 初始化
boids = [Boid(np.random.uniform(0, width), np.random.uniform(0, height)) for _ in range(num_boids)]
fig, ax = plt.subplots(figsize=(6, 6))
# 獲取初始位置和速度
initial_positions = np.array([b.position for b in boids])
initial_velocities = np.array([b.velocity for b in boids])
scatter = ax.scatter(initial_positions[:, 0], initial_positions[:, 1], c='steelblue', s=30)
quiver = ax.quiver(initial_positions[:, 0], initial_positions[:, 1],
initial_velocities[:, 0], initial_velocities[:, 1],
color='steelblue', scale=50, alpha=0.7)
ax.set_xlim(0, width)
ax.set_ylim(0, height)
ax.set_title('Boids Simulation')
ax.set_aspect('equal')
def update(frame):
for boid in boids:
neighbors = [b for b in boids if b != boid and np.linalg.norm(b.position - boid.position) < 15]
if neighbors:
# 分離:遠離太近的同伴
separation = np.zeros(2)
for n in neighbors:
diff = boid.position - n.position
dist = np.linalg.norm(diff)
if dist < 5:
separation += diff / (dist + 0.1)
# 整列:趨向附近同伴的平均速度
alignment = np.mean([n.velocity for n in neighbors], axis=0)
# 結合:朝向群體的中心
cohesion = np.mean([n.position for n in neighbors], axis=0) - boid.position
# 合成力量
boid.velocity += separation * 0.05 + alignment * 0.05 + cohesion * 0.01
# 限制速度
speed = np.linalg.norm(boid.velocity)
if speed > 4:
boid.velocity = boid.velocity / speed * 4
# 更新位置(邊界環繞)
boid.position = (boid.position + boid.velocity) % [width, height]
positions = np.array([b.position for b in boids])
velocities = np.array([b.velocity for b in boids])
scatter.set_offsets(positions)
quiver.set_offsets(positions)
quiver.set_UVC(velocities[:, 0], velocities[:, 1])
return scatter, quiver
anim = FuncAnimation(fig, update, frames=steps, interval=50, blit=True)
plt.close()
return HTML(anim.to_jshtml())
# 執行
boids_simulation(num_boids=50, steps=200)</details>
③ Tierra(1990 年)
由生態學家托馬斯·S·雷開發的系統,用於觀察計算機上的基因突變。
"Tierra" 在西班牙語中意味著「地球」。
Tierra 的規則
在 Tierra 中,將執行自我複製的單個程序(基因代碼)視為「虛擬生物」。
- 自我複製:虛擬生物使用 CPU 時間(能量)和記憶體空間(生存區域)進行自我複製
- 死亡:當記憶體使用超過 80% 時,「死神」(Reaper)會出現,並從舊個體或錯誤多的個體中刪除
- 突變:模擬宇宙射線,在自我複製時以一定概率反轉基因代碼(CPU 指令)的位元
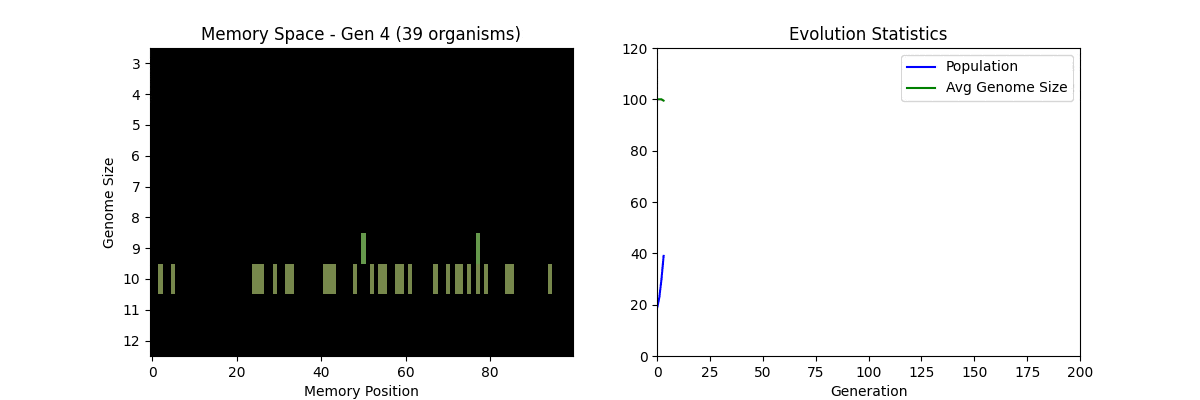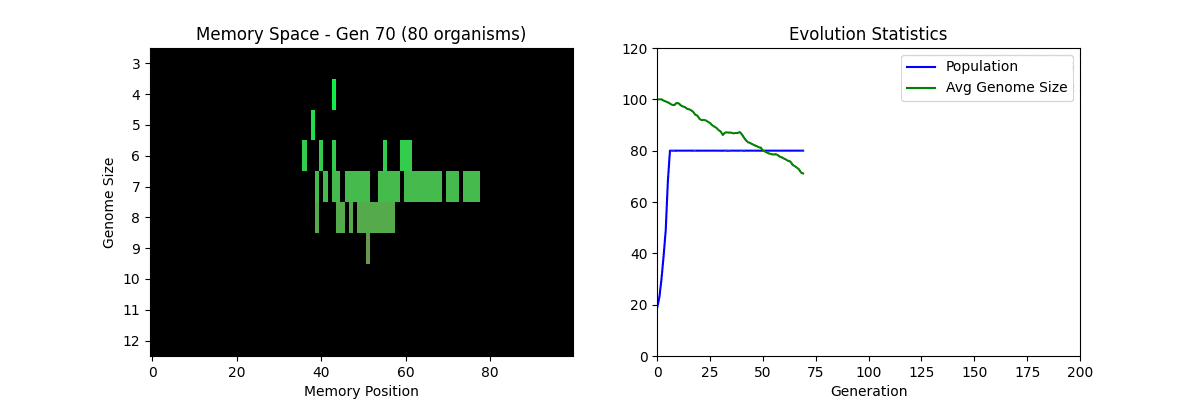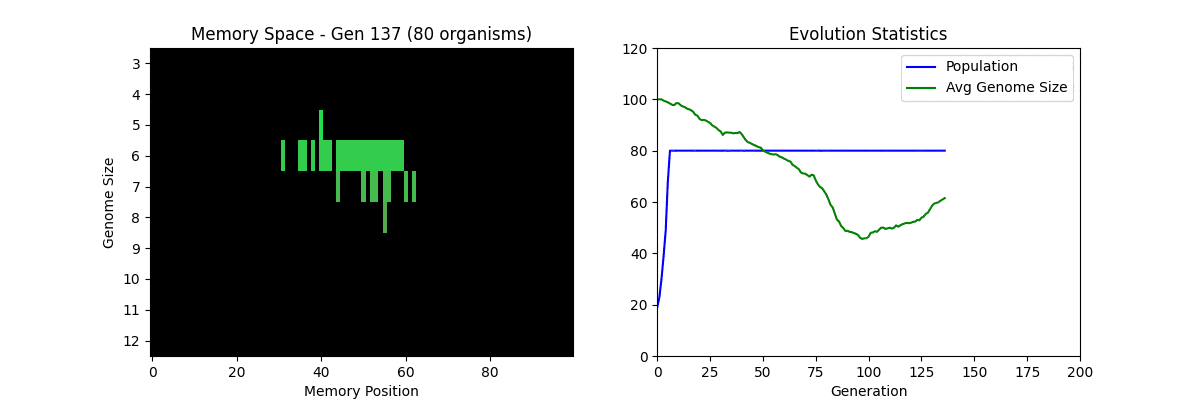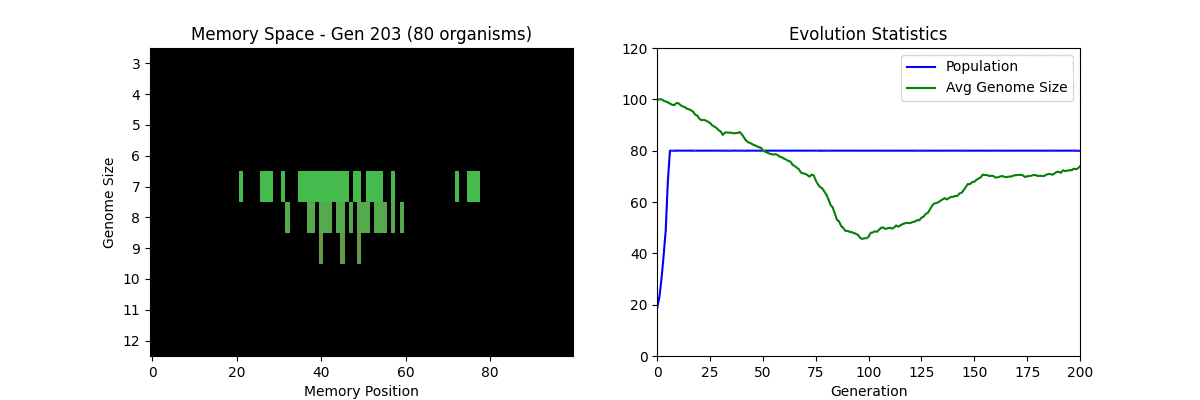
嘗試 Tierra(簡易版)
原本的 Tierra 是一個在實際記憶體上執行 CPU 指令(機械語)的自我複製系統。
在這裡為了幫助理解概念,我們用 Python 的列表來表現「基因組」的簡易版。
💡 左側的記憶空間顯示了生物的分佈。上方=有效率(短基因組),下方=低效率(長基因組)。可以確認隨著進化,有效率的短基因組虛擬生物逐漸增多(被選擇)。
<details>
<summary>Python 程式碼</summary>
import random
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
from matplotlib.colors import LinearSegmentedColormap
from collections import Counter
from IPython.display import HTML
class Organism:
"""數位生物:擁有基因組(指令序列)並能自我複製"""
def __init__(self, genome=None, position=None):
if genome is None:
self.genome = [random.randint(0, 9) for _ in range(10)]
else:
self.genome = genome.copy()
self.age = 0
self.errors = 0
self.position = position if position else random.randint(0, 99)
def replicate(self, mutation_rate=0.02):
"""自我複製(含突變)"""
new_genome = []
for gene in self.genome:
if random.random() < mutation_rate:
mutation_type = random.choice(['change', 'insert', 'delete'])
if mutation_type == 'change':
new_genome.append(random.randint(0, 9))
elif mutation_type == 'insert':
new_genome.append(gene)
new_genome.append(random.randint(0, 9))
else:
new_genome.append(gene)
if len(new_genome) < 3:
return None
return Organism(new_genome, position=(self.position + random.randint(-5, 5)) % 100)
def fitness(self):
bonus = self.genome.count(7) * 2
return 100 - len(self.genome) + bonus - self.errors
def get_color(self):
"""基於基因組大小的顏色(短的=上、長的=下)"""
size = len(self.genome)
ratio = min(1.0, max(0.0, (size - 3) / 15))
return (ratio, 1 - ratio, 0.3)
class TierraVisualSimulation:
def __init__(self, memory_size=100, initial_population=10):
self.memory_size = memory_size
self.memory_width = 100
self.organisms = []
self.generation = 0
for _ in range(initial_population):
self.organisms.append(Organism())
def step(self):
self.generation += 1
for org in self.organisms:
org.age += 1
if random.random() < 0.01:
org.errors += 1
offspring = []
for org in self.organisms:
if random.random() < 0.3:
child = org.replicate()
if child:
offspring.append(child)
self.organisms.extend(offspring)
while len(self.organisms) > self.memory_size:
self.organisms.sort(key=lambda o: o.fitness() - o.age * 0.5, reverse=True)
self.organisms.pop()
def get_memory_view(self):
"""生成可視化的記憶空間數據"""
memory = np.zeros((10, self.memory_width, 3))
for org in self.organisms:
x = org.position % self.memory_width
y = min(9, len(org.genome) - 3)
color = org.get_color()
memory[y, x] = color
return memory
def animate(self, steps=200):
"""動畫顯示"""
fig, axes = plt.subplots(1, 2, figsize=(12, 4))
# 記憶視圖
memory_img = axes[0].imshow(self.get_memory_view(), aspect='auto')
axes[0].set_title('記憶空間 (Y=基因組大小, 顏色=適應度)')
axes[0].set_xlabel('記憶位置')
axes[0].set_ylabel('基因組大小')
axes[0].set_yticks(range(10))
axes[0].set_yticklabels(range(3, 13))
# 統計圖表
pop_line, = axes[1].plot([], [], 'b-', label='種群')
size_line, = axes[1].plot([], [], 'g-', label='平均基因組大小')
axes[1].set_xlim(0, steps)
axes[1].set_ylim(0, 120)
axes[1].set_xlabel('世代')
axes[1].legend()
axes[1].set_title('進化統計')
history = {'pop': [], 'size': []}
def update(frame):
self.step()
# 更新記憶視圖
memory_img.set_array(self.get_memory_view())
# 更新統計
if self.organisms:
history['pop'].append(len(self.organisms))
avg_size = sum(len(o.genome) for o in self.organisms) / len(self.organisms)
history['size'].append(avg_size * 10) # 調整比例
else:
history['pop'].append(0)
history['size'].append(0)
pop_line.set_data(range(len(history['pop'])), history['pop'])
size_line.set_data(range(len(history['size'])), history['size'])
axes[0].set_title(f'記憶空間 - 第 {self.generation} 世代 ({len(self.organisms)} 個生物)')
return memory_img, pop_line, size_line
anim = FuncAnimation(fig, update, frames=steps, interval=50, blit=True)
plt.close()
return HTML(anim.to_jshtml())
# 執行
sim = TierraVisualSimulation(memory_size=80, initial_population=15)
sim.animate(steps=200)</details>
前篇總結
本文介紹了 ALIFE 的三個代表性模擬。
| 模擬 | 年代 | 創發的現象 |
|---|---|---|
| 生命遊戲 | 1970年 | 從簡單的規則中產生複雜的模式 |
| Boids | 1986年 | 個體的局部判斷產生群體行為 |
| Tierra | 1990年 | 從自我複製和淘汰中產生進化 |
可以共同指出的是,簡單的規則可以創發出複雜的行為。
這就是 ALIFE 的奇妙之處,或許正是因為歷經數億年的重複,最終導致了人類這一奇特的創造。
=>後篇繼續👉
參考文獻
原文出處:https://qiita.com/watanabe_masaru/items/a37506c1acda0307d8aa
1) --- 會變成分隔線(上一行必須是空白)
2) # 會變成一級標題
3) ## 會變成二級標題
4) ### 會變成三級標題
5) **粗體文字**會顯示粗體文字
6) ```當第一行與最後一行會顯示程式碼
7) 請搜尋 Markdown 語法,了解各種格式
