🔧 阿川の電商水電行

投資不致破產的數學:理解ケリー基準
前言:為何優秀的交易者也會破產
在投資的世界中,存在著一種奇妙的現象。勝率高達55%,即贏的次數多於輸的交易者,卻有可能破產。另一方面,即便勝率相同,但能穩定增長資產的投資者卻屢見不鮮。這種差異究竟是什麼呢?
答案在於「持倉規模」。無論有多優秀的投資策略,只要一時賭注大小不當,最終都可能會失去資產。反之,即便勝率不算高,只要進行適當的資金管理,長期也能獲得成功。
本文將以Python模擬為例,解釋1956年貝爾研究所的約翰·L·ケリー·ジュニア所發現的「ケリー基準(Kelly Criterion)」。這一數學方法能指導我們如何在長期內最高效率地增加資產。
本文學習要點
- ケリー基準的數學意義與公式
- 為何過度賭注會導致破產
- Python模擬的實證結果
- 在實際投資中的應用方法
ケリー基準的基本概念:從簡單的例子開始理解
首先,想像一個非常簡單的賭博遊戲。我們投擲硬幣,如果出現正面,賭金翻倍;如果出現反面則失去全部賭金。然而,這枚硬幣並非普通的硬幣,而是有55%的機率出現正面的稍微有利的硬幣。
手中擁有100萬元,當我們重複這個遊戲250次時,每次應該賭多少才是最佳選擇呢?
直覺上可能會認為「勝率高達55%時,賭得越多越能獲利」。但是,這是一個巨大的誤解。實際模擬的結果會讓我們驚訝不已。
ケリー基準的公式
ケリー基準的公式如下:
f^* = \frac{bp - q}{b}其中,
- $f^*$:應該賭的資產比例
- $p$:勝率
- $q = 1 - p$:失率
- $b$:賠率(在此例中為1,即贏得2倍)
將我們的例子(勝率55%,1:1的賠率)代入公式:
f^* = \frac{1 \times 0.55 - 0.45}{1} = 0.10也就是說,每次賭注為資產的10%是最佳選擇。
重要的點
即使勝率為55%,最優賭注比例也僅為10%。這一數字遠比直覺所想要低得多。
使用Python模擬進行驗證
僅憑理論可能難以產生實感,讓我們來實際進行模擬。下面提供的代碼將在不同投注比例下重複進行數千次遊戲,並可視化結果。
ケリー係數的計算
def kelly_fraction(p: float, b: float = 1.0) -> float:
"""計算ケリー係數的函數
Args:
p: 勝率
b: 賠率(贏時的倍數 - 1)
Returns:
最優賭注比例
"""
q = 1.0 - p # 失率
return (b * p - q) / b在這次模擬中,我們將進行5000次嘗試,追蹤每種賭注比例所帶來的結果。重要的是使用「預期對數增長率」這一指標,而非簡單的平均值。
為何對數增長率如此重要
在投資的世界中,「複利效應」意義重大,而非單純的平均利潤。100萬元翻倍變為200萬元,若再度翻倍則為400萬元。這種乘法增長方式需要透過對數進行恰當處理。
預期對數增長率的公式為:
g(f) = p \log(1 + bf) + (1-p) \log(1 - f)最大化該函數的 $f$ 便是ケリー係數 $f^*$。從模擬產生的左側圖表可見,所描繪的曲線與理論完全一致。
模擬結果所帶來的三個重要教訓
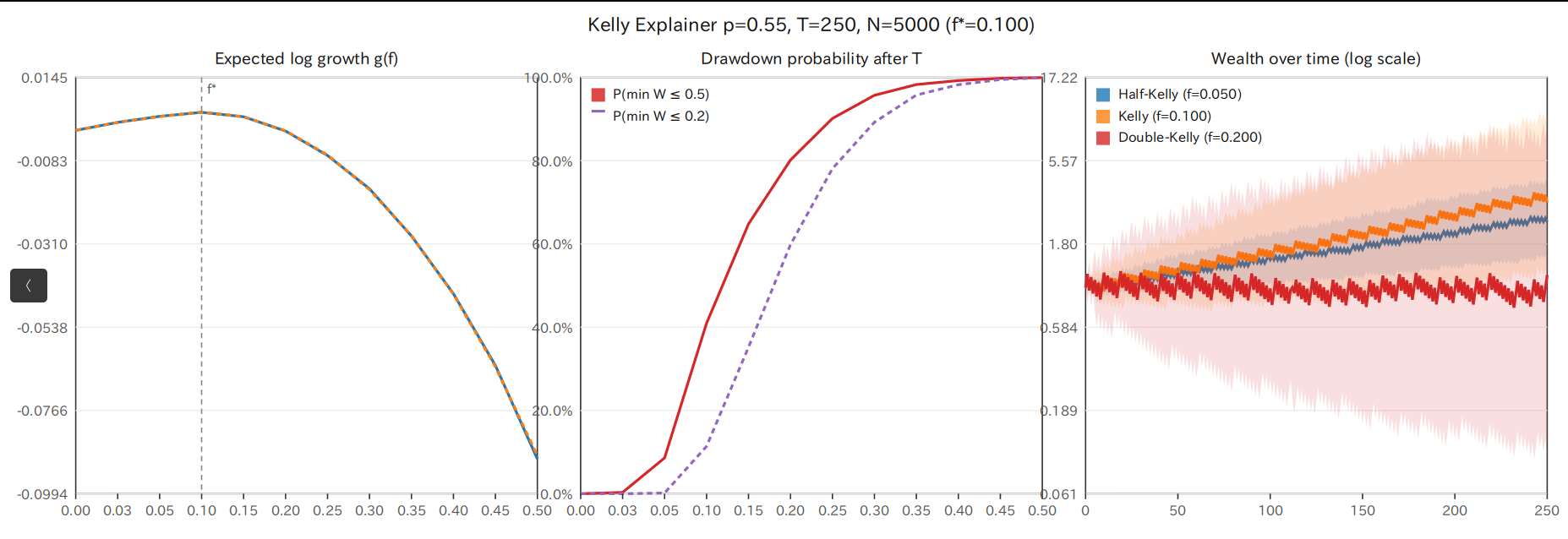
第一教訓:超過最優值後增長率會急劇下降
仔細觀察圖表左側的面板。藍色實線代表模擬的實際結果,橙色虛線則是理論值。兩者幾乎完全一致,展示出理論的正確性。
引人注意的是,ケリー係數(在此為0.10)時增長率達到最大,超過此值後則急劇下降。例如,若賭注提高至0.20,增長率便會變為負數。這意味著,長期而言,資產必然會減少。
勝率55%時即使賭20%也會虧損
「明明勝率有55%,賭20%卻會虧損」這看似矛盾,但這正是複利的恐怖之處。一旦出現大額虧損,便需要數倍的利潤來彌補。
第二教訓:過度賭注可能導致災難性損失
中央的圖表展示了更震驚的事實。這是「回撤概率」,顯示資產跌落至某一水平以下的概率。
紅色實線表示「資產低於原先50%以下的概率」。若賭注為ケリー係數的兩倍(0.20),在250次遊戲中,資產幾乎以100%的概率降到一半以下。紫色虛線所示的「損失80%」也以高概率發生。
這並非理論上的討論。實際投資中,過度槓桿的交易者經常在短期內獲利後,卻因一次暴跌而損失全部。
第三教訓:隨著時間推移,差距以指數方式擴大
右側的圖表展示了最具啟示性的結果。這是隨時間變化資產如何變化的三個策略的比較。
| 策略 | 賭注比例 | 特點 |
|---|---|---|
| 半ケリー | 0.05 | 非常穩定,但增長緩慢 |
| ケリー | 0.10 | 平衡且穩定增長 |
| 雙ケリー | 0.20 | 變化劇烈,資產多數情況下減少 |
值得注意的是,色彩帶顯示的範圍,代表著25百分位數到75百分位數,即中間50%的案例所落入的範圍。雙ケリー的範圍相當寬廣,顯示出明顯的不穩定性。
隨著時間的推移,適當的賭注比例與不適當賭注比例之間的差距會劇烈擴大。這便是複利的力量。
實踐應用:將理論運用於現實投資
至此,您應該已經理解了ケリー基準的理論。然而,將其運用於實際投資還需要考慮幾個關鍵要素。
勝率估算的難題
ケリー基準的最大弱點在於需要知道準確的勝率。模擬中勝率設為55%,但在實際投資中準確掌握勝率幾乎是不可能的。
如果高估勝率會發生什麼情況呢?假如實際勝率為50%(即沒有優勢),但認為勝率為55%而持續投注10%。此時,ケリー基準應該會顯示 $f^* = 0$,但實際上已經賭了10%,長期下來將必然遭受損失。
推薦半ケリー策略
許多實務工作者推薦「半ケリー」或「四分之一ケリー」,因為投注理論上最優值的一半或四分之一,能為估算誤差提供保障。
若有多個投資機會
在實際投資中,不僅僅是單一遊戲,而是存在多個投資機會。股票、債券、商品、外匯等皆有不同的勝率和賠率。
此時,應對每個投資機會應用ケリー基準,並計算各自的建議持倉規模。然而,簡單地將所有持倉加總可能會導致總持倉超過100%。
這一問題可以透過約束最優化的數學方法來解決。也就是在「所有持倉總和不超過100%」的條件下最大化預期對數增長率。這與現代投資組合理論之間存在有趣的接點。
心理層面:理論與實踐的差異
無論多麼優秀的數學方法,如果不能實行也是無用的。ケリー基準面臨的一大挑戰在於其建議的持倉規模對多數人來說可能過於龐大。
例如,若存在勝率60%、賠率2:1的極有利投資機會,凯利基準建議賭注為33%,即資產的三分之一。然而,將資產的三分之一投資於單一項目,對於許多人來說,心裡會有很大的抵觸。
這涉及到「風險容忍度」的問題。即便數學上最優,還是無需承擔會讓人夜不能寐的風險。半ケリー或四分之一ケリー是在稍稍放鬆數學效率的情況下,以獲得心理穩定的妥協。
代碼詳細:模擬的工作原理
提供的Python代碼以非常精緻的方式模擬了ケリー基準。接下來讓我們來看看幾個重要的部分。
蒙特卡羅模擬
def run_sim(
p: float = 0.55,
T: int = 250,
N: int = 5000,
b: float = 1.0,
fractions: List[float] = None,
seed: int = 42,
) -> Tuple[List[Dict], float]:
# 對每一賭注率執行5000次試驗
for f in fractions:
wealths: List[float] = []
log_growths: List[float] = []
for i in range(N):
# 在每次試驗中執行250次遊戲
w = 1.0 # 初始資產
lg = 0.0 # 對數增長率的累積
for _ in range(T):
if rng.random() < p:
factor = 1.0 + b * f # 贏
else:
factor = 1.0 - f # 輸
w *= factor # 更新資產
lg += math.log(factor) # 累積對數增長率這段代碼的巧妙之處在於對破產的處理。賭注過高時,資產可能為零或負數。在這種情況下,將對數增長率設為一個非常大的負數(-1e9),以適當反映破產的懲罰。
時間序列數據的生成
def time_quantiles(
p: float,
T: int,
N: int,
b: float,
f_values: List[float],
seed: int,
qs: Tuple[float, float, float] = (0.25, 0.5, 0.75),
) -> Dict[float, Dict[str, List[float]]]:
# 計算各時間點的25、50、75百分位數該函數追蹤隨著時間變化資產分布的情況。這使我們能夠描繪出右側圖表的色彩帶(四分位範圍)。藉由不僅查看中位數,還能觀察分布的廣度,幫助我們更深刻理解策略的風險特性。
SVG輸出:無依賴的可視化
這段代碼的另一個特點是,直接生成SVG而非使用外部庫(如matplotlib)。這樣可以將依賴減至最低,同時創建美觀的圖表。
def save_svg(path: str, results: List[Dict], meta: Dict) -> None:
# 定義坐標轉換
def xmap(idx: int, panel: int) -> float:
t = 0.0 if len(fs) == 1 else idx / (len(fs) - 1)
return margin + panel * (panel_w + gutter) + t * panel_w
def y_g(v: float) -> float:
return margin + (1 - (v - g_min) / (g_max - g_min)) * panel_h這部分定義了數據空間到像素空間的轉換。在數學上這是一種線性轉換,將數據的最小值和最大值映射到屏幕的上端和下端。
深入理解:數學背景
ケリー基準背後的數學與信息論有著密切的關聯。事實上,ケリー的原始論文是以信息傳播的背景寫成的。
最大化預期對數增長率與最大化熵是等價的。更準確地說,ケリー基準被解釋為優化賭注所帶來的信息,及其將該信息轉化為資產增長的效率。
與中心極限定理的關係
在足夠長的時間內,對數資產近似服從正態分布。這是中心極限定理的結果。ケリー基準可以看作是最大化該正態分布平均值的策略。
但需注意的是,這僅是「期望值」的最大化,並非「中位數」或「最頻值」的最大化。從右側圖表可見,雙ケリー的中位數低於ケリー,這表示雙ケリー在少數幸運案例中提升了平均值,但在典型案例中卻不如ケリー。
從風險調整後收益的觀點看
在現代投資理論中,像夏普比率等風險調整後的收益受到重視。ケリー基準被認為是基於假設的對數效用函數的最佳策略。
對數效用函數代表了風險規避的投資者。資產翻倍所帶來的快樂,遠不如資產減半所引起的悲傷。這在數學上反映了人類的心理。因此,ケリー基準不僅僅是數學最佳化的策略,更是一種反映人性心理的實用手段。
總結:從ケリー基準中學到的要點
通過本文,我希望您已經理解了ケリー基準不僅是一個賭金計算公式,而是投資底層原理的體現。
最重要的教訓
即使擁有優勢,過度賭注也不可取
數學上證實的最佳值,從實務上來看,建議將其減半。這是對不確定性及人類極限的謙卑認識的表現。
此外,「時間是最強的武器」這一觀點也不容忽視。適當的資金管理下,即使只有微小的優勢,也能隨著時間推移產生巨大的差距。相反,不恰當的資金管理則會使任何優勢化為烏有。
最後,理論與實踐之間的平衡也十分關鍵。ケリー基準是優美的理論,但我們不能盲目循從,而要考慮自身的風險容忍度、預估不確定性及市場特性,進而適當調整。
投資成功的公式
若要概括投資成功的公式,可為以下形式:
成功 = 優勢 × 合適的持倉規模 × 時間 × 紀律ケリー基準是這一公式中第二項的強有力工具。然而,其他要素,特別是最後的「紀律」,同樣重要。再優秀的策略也需一貫執行,否則將毫無意義。
實際嘗試
建議您實際運行模擬代碼,測試不同的參數。改變勝率或賠率,能讓您對ケリー基準的行為有更深入的理解。
執行命令
# 模擬的執行示例
python simulate_kelly.py --p 0.55 --T 250 --N 5000這個命令執行後,將在kelly目錄中生成結果的CSV文件和精美的SVG圖。請您仔細欣賞這些結果,並思考長期資產增長的策略。您一定會獲得新的見解。
參考文獻
- Kelly, J. L. (1956). "A New Interpretation of Information Rate". Bell System Technical Journal.
- Thorp, E. O. (2006). "The Kelly Criterion in Blackjack Sports Betting, and the Stock Market".
- MacLean, L. C., Thorp, E. O., & Ziemba, W. T. (2011). "The Kelly Capital Growth Investment Criterion".
1) --- 會變成分隔線(上一行必須是空白)
2) # 會變成一級標題
3) ## 會變成二級標題
4) ### 會變成三級標題
5) **粗體文字**會顯示粗體文字
6) ```當第一行與最後一行會顯示程式碼
7) 請搜尋 Markdown 語法,了解各種格式

